什么是格雷码?
格雷码(Gray Code)是一种二进制数编码方法,具有以下特点:在相邻的两个数之间,只有一位二进制位发生变化。这种特性使得格雷码在某些应用中非常有用,尤其是在数字电路和数据传输中,能够有效减少错误的发生。
格雷码的基本概念
定义:格雷码是一种编码系统,其中两个连续数的二进制表示形式仅在一个比特位上有所不同。例如,二进制数000和001的格雷码分别为000和001,而001和010的格雷码则为001和011。
转换方法:
对于任意一个二进制数,格雷码的第一位与其二进制数的第一位相同。
后续的每一位格雷码为当前二进制数对应位与前一位的异或(XOR)结果。
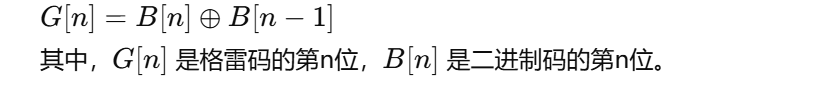
示例
考虑4位二进制数及其对应的格雷码:
| 二进制 | 格雷码 |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
应用场景
数字电路:在旋转编码器和模拟量转换器中,使用格雷码可以避免在值变化时出现的误读。
数据传输:在数据传输过程中,格雷码可以减少因电信号噪声导致的错误。
图形处理:在计算机图形学中,格雷码用于表示空间中对象的运动,以减少运动模糊。
总结
格雷码是一种重要的编码方式,具有在特定条件下的优越性。了解格雷码的原理和应用有助于在相关领域的深入研究和实践。
转换步骤
确定二进制数:首先,准备要转换的二进制数。例如,假设要转换的二进制数是
1011。第一位保持不变:格雷码的第一位与二进制数的第一位相同。对于
1011,第一位是1,所以格雷码的第一位也是1。后续位的计算:
对于后续的每一位,使用当前位和前一位的异或运算(XOR)。
记住:如果两个位相同,结果是
0;如果不同,结果是1。
详细示例
以二进制数 1011 为例,逐步转换为格雷码:
第一位:
二进制的第一位是
1→ 格雷码的第一位是1第二位:
二进制的第二位是
0,前一位是1计算:
1 XOR 0 = 1→ 格雷码的第二位是1第三位:
二进制的第三位是
1,前一位是0计算:
0 XOR 1 = 1→ 格雷码的第三位是1第四位:
二进制的第四位是
1,前一位是1计算:
1 XOR 1 = 0→ 格雷码的第四位是0
最终结果
将上述计算结果结合起来,得到的格雷码为 1110。
转换格雷码时,从左往右进行操作。
转换步骤总结:
第一位:直接复制二进制数的第一位。
后续位:从第二位开始,使用前一位和当前位进行异或(XOR),从左到右依次计算。
所以,转换时确实是从左到右进行的。这样能够确保每一位都正确计算。

- 上一篇:c语言求素数
- 下一篇:arduino按键控制led灯
